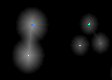Introduction to computerized image analysis

Feature extraction

When we have segmented our images, we often want to calculate various features for the different regions. It can have to do with size or shape. One common tool to analyze a region is to calculate the distance transform of the region. This means that we create a new image where all pixels outside the region, i.e., in the background, have value 0 and a pixel in the region is given the value of the distance from it to its closest pixel in the background. Below we see the image with the discs again. If we compute the distance transform of the "disc region" we obtain the image to the right. In that image we can, for instance, search for all maxima. When we find a maximum in the distance transform we know that we are in the middle of a disc and by the value of the pixel we also know the size of the disc.

Discs	Segmentation	Distance transform

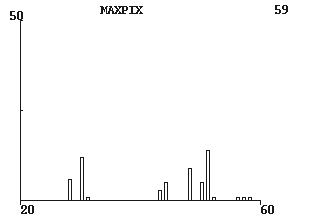
The discs in the image above are of different sizes. To figure out how many discs there are of each size and in that way classify the discs we can use the maxima in the distance transform and labelling. We start by detecting all maxima in the distance transform and assign them different labels in the computer. This we need to do to distinguish and keep track of individual discs. Below to the left we see part of the disc image. The lightest pixels, i.e., the maxima, are shown in colour. The colour indicates the label the pixel has in the computer. After this we compare the maxima for the different labels. The result is shown in the histogram below.

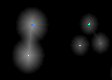Maxima detected and labelled	Histogram of the size of the discs

It is possible to find certain boundaries in the histogram. One group seems to be around radius 30, one around radius 44 and one around radius 50. Moreover there are a few with radius >50.

There are also other ways of measuring the shape of the region we have segmented. One which is common to use is the P²/A measure. This means that we compute P=perimeter och A=area for the region/object. The actual measure is P²/A= P*P/A. It is a measure of "roundness" or compactness. We note that for a disc holds P²/A=(2*pi*r)²/(pi*r²)=4*pi, where r is the radius. If we have something with the same perimeter as a disc, but that is more shaped as an oval then P²/A>4*pi, as an example see the disc and ellips below.

perimeter=2pi	perimeter=2pi
area=pi	area=3pi/4

One example where this can be used is to distinguish between pine and spruce. From above a pine looks rounded, while a spruce is more straggling. This means that for pine P²/A is close to 4pi while for spruce it is much larger than 4pi, as the area is small while the perimeter is large.

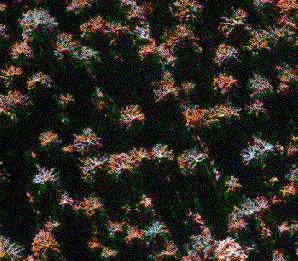mostly pine	only spruce