|
The Stochastic Watershed
Bettina Selig, Cris Luengo, Ida-Maria Sintorn, Filip Malmberg, Robin Strand
Funding: S-faculty, SLU
Period: 1102-
Abstract: The stochastic watershed is a method recently presented that builds on the classical seeded watershed algorithm. It creates a probability density function for edges in the image by repeated applications of the seeded watershed with random seeds. Previously, we developed a perturbation-based approach to improve the properties of the algorithm: by adding noise to the input image at every application of the seeded watershed, we were able to avoid larger regions being split.
During 2014, we published an efficient, deterministic algorithm that computes the result that one would obtain after an infinite number of repetitions of the seeded watershed (Pattern Recognition Letters), as well as an efficient algorithm to convert this tree-based result back to all edges in the image's graph.
We also submitted a paper that describes a method to combine the perturbation-based approach with the deterministic algorithm. This combined method is much faster than the original perturbation-based method, and improves on its results slightly.
Adaptive Mathematical Morphology
Vladimir Curic, Cris Luengo, Gunilla Borgefors
Partners: Anders Landström, Matthew Thurley, Luleå University of Technology, Luleå; Sébastien Lefèvre, University of South Brittany, Vannes, France; Jesús Angulo, Santiago Velasco-Forero, Centre for Mathematical Morphology, MINES ParisTech, Fontainebleau, France
Funding: Graduate School in Mathematics and Computing (FMB)
Period: 1101-
Abstract: The construction of adaptive structuring elements that adjust their shape and size to the local structures in the image has recently been a popular topic in mathematical morphology. Despite that several methods for the construction of spatially adaptive structuring elements have been proposed, it is still an open problem, both from a theoretical and implementation point of view. We have proposed the salience adaptive structuring elements, which modify their shape and size according to the saliency of nearby edges in the image, as well as structuring element with a predefined shape that only changes size based on the saliency of nearby edges.
This year, we published an overview paper on adaptive mathematical morphology, in which we compared a few of the most important methods for constructing adaptive structuring elements, as well as theoretical advances on how to properly define morphological operators. Currently, we are working towards defining more complex morphological operators using adaptive structuring elements, such as an adaptive hit-or-miss transform. Vladimir Curic defended his PhD thesis closely linked to this project in May 2014.
Digital Distance Functions and Distance Transforms
Robin Strand, Gunilla Borgefors
Partner: Benedek Nagy, Dept. of Computer Science, Faculty of Informatics, University of Debrecen, Hungary; Nicols Normand, IRCCyN, University of Nantes, France
Funding: TN-faculty, UU; S-faculty, SLU
Period: 9309-
Abstract: The distance between any two grid points in a grid is defined by a distance function. In this project, weighted distances have been considered for many years. A generalization of the weighted distances is obtained by using both weights and a neighborhood sequence to define the distance function. The neighborhood sequence allows the size of the neighborhood to vary along the paths.
In 2014, the work was focused on weight sequence distance functions, where weighted neighborhood sequences of infinte length are allowed.
The Minimum Barrier Distance
Robin Strand, Filip Malmberg, Elisabeth Linnér
Partners: Punam K. Saha, Dept. of Electrical and Computer Engineering and the Dept. of Radiology, University of Iowa, IA, USA; Krzysztof C. Ciesielski, Dept. of Mathematics, West Virginia University, Morgantown, WV, USA; Dept. of Radiology, MIPG, University of Pennsylvania, PA, USA
Funding: TN-faculty, UU
Period: 1103-
Abstract: In this project, we introduce a distance function on a fuzzy subset that gives the minimum barrier that has to be passed to go from one point to another. Theoretical properties as well as efficient computational solutions for minimum barrier distance have been developed. An initial application of minimum barrier distance in image segmentation is presented. The experiments show that the minimum barrier distance is robust to noise and blur, and also seed point position, since it captures the total change in membership values across an interface instead of gradient as a measure of slope that is sensitive to noise and blur.
During 2014, a paper describing an efficient method for exact calculation of minimum barrier distance transforms was published in Computer Vision and Image Understanding. Another paper, published in the proceedings of the international conference on Discrete Geometry for Computer Imagery, investigated the stability of the minimum barrier distance with respect to seed point position.
Set Distances and their Application in Image Analysis
Vladimir Curic, Gunilla Borgefors, Nataša Sladoje
Partner: Joakim Lindblad, Faculty of Technical Sciences, University of Novi Sad, Serbia
Funding: Graduate School in Mathematics and Computing (FMB); TN-faculty, UU
Period: 0908-1406
Abstract: We have, in 2014, concluded our study related to methods for
measuring distances between sets, summarizing the results in two journal
publications and in Vladimir's PhD thesis, successfully defended in May
2014. To measure how similar sets are can be useful for solving various
image analysis related problems, such as registration, image retrieval and
segmentation evaluation.
During the project, we have evaluated existing and developed new set distances which are useful in image registration related problems. A new set distance between crisp sets of points is presented and evaluated w.r.t. utiliziation in rigid body registration of binary images, as well as for multi-modal 2D-3D registration of 2D histological sections of bone implant with corresponding 3D synchrotron radiation micro computed tomography (SRµCT) bone implant volumes. This work is published in the Pattern Analysis and Applications journal.
We extended our study to fuzzy objects and proposed four novel point-to-set distances defined for fuzzy or gray-level image data, two based on integration of alpha cuts and two based on the fuzzy distance transform. We further used these point-to-set distances to define distances between fuzzy sets. Theoretical study and performance evaluation of the proposed distances con- firm their excellent behaviour in template matching and object classification. New distance measures enable inclusion of both spatial and intensity information, which makes them applicable to texture matching problems as well. The results of this study are published in IEEE Transactions on Image Processing. Vladimir defended his PhD thesis closely linked to this project in 2014.
Direct Curvature Calculation of Surfaces in 3D Volumes
Erik Wernersson, Cris Luengo, Anders Brun, Gunilla Borgefors
Funding: S-faculty, SLU
Period: 1009-1412
Abstract: Curvature is known to be a useful local descriptor of 2D surfaces, embedded in 3D space. Not only for parametric surfaces but also estimated from objects in digital images with applications ranging from visualisation to segmentation. Within this project, we have studied curvature calculated from the structure tensor, in contrast to the most common methods which derive curvature directly from image differentials. Using the structure tensor, we were able to use non-standard derivative operators to determine curvature. We also used non-linear smoothing to create the structure tensor. These two modifications together allow for a more precise estimate of curvature in places where the curvature changes quickly, or where two surfaces of different curvature are close together. We also correctly determine the sign of the curvature, which allows us to distinguish concave and convex surfaces. This distinction is useful for example to differentiate the inner and outer surface of a wood fibre. Erik defended his PhD thesis closely linked to this project in December of 2014.
Image Enhancement based on Energy Minimization
Nataša Sladoje
Partners: Joakim Lindblad, Buda Bajic, Faculty of Engineering, University of Novi Sad, Serbia
Funding: Swedish Governmental Agency for Innovation Systems (VINNOVA); TN-faculty, UU
Period: 1409-
Abstract: A common approach to solve the very important but severely ill-posed problem of image deconvolution, is to formulate it in a form of an energy minimization problem. Typically, some regularization is applied, utilizing available a priori knowledge. Total variation regularization is among most popular approaches, due to its generally good performance.
Within this project we are exploring different ways to improve the results of energy minimization based image deconvolution. During 2014 we have studied utilization of different potential functions in restoration of images degraded by both noise and blur. We have tested performance of seven known potentials, convex as well as non-convex, utilizing empirically determined optimal parameter settings for each of them. We have performed optimization by a flexible and efficient SPG method. Our study confirm that some appropriately chosen potentials provide a straightforward way to increase quality of the restored images.
We have presented the results of our study at the International Conference on Image Analysis and Recognition (ICIAR 2014), held in Algarve, Portugal.
The proceedings of the conference is printed in the Lecture Notes in Computer Science series.
Coverage Model and its Application to High Precision Medical Image Processing
Nataša Sladoje
Partners: Joakim Lindblad, Faculty of Technical Sciences, University of Novi Sad, Serbia; Attila Tanács and Zoltan Kato, Dept. of Image Processing and Computer Graphics, University of Szeged, Hungary
Funding: TN-faculty, UU
Period: 1409-
Abstract: The coverage model, that we have been developing for several years now, provides a framework for representing continuous objects present in digital images as spatial fuzzy subsets. Assigned membership values indicate to what extent image elements are covered by the imaged objects. During last years, we have shown, both theoretically, and in applications, that the model can be used to improve information extraction from digital images and to reduce problems originating from limited spatial resolution.
During 2014, we have finalized our study on a unified framework to recover linear geometric correspondences between binary objects in -dimensions. The solution of the registration problem is obtained by solving polynomial systems of equations that are based on geometric moments of the template and observation, with no need for additional correspondences.
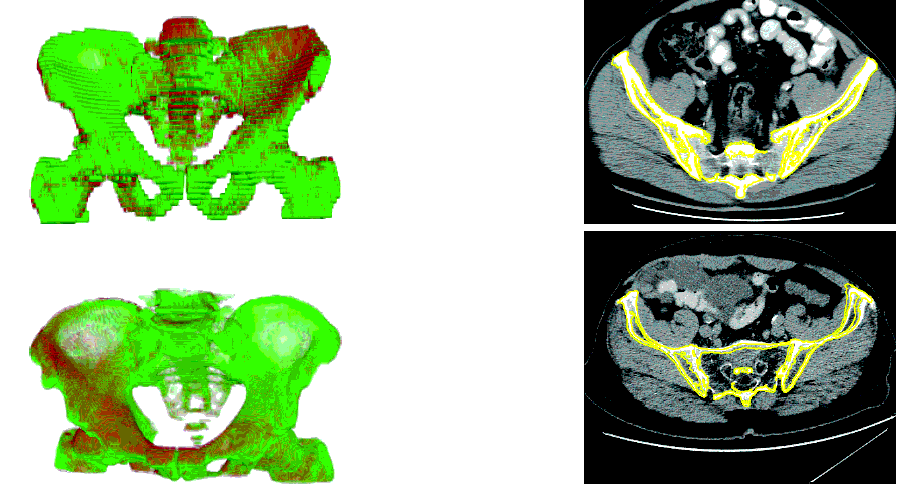
To further improve the performance of this fast and efficient registration method, we have proposed to use coverage information to compensate for possibly insufficient spatial resolution and to reach the desired precision of moments estimates. The work is published in the Pattern Recognition journal, where the advantages of this approach are clearly demonstrated, in particular in terms of increased percentage of registration results in the highest scoring group. An illustration of the proposed methods is demonstrated on real X-ray images of hip replacement implants and 3D CT volumes of the pelvic area (Figure 22).

|
|
|
|
|
|
|
Digital Hyperplanes
Christer Kiselman
Partner: Adama Koné, Université de Bamako
Funding: International Science Programme; Université de Bamako; Kingdom of Sweden
Period: 1011-
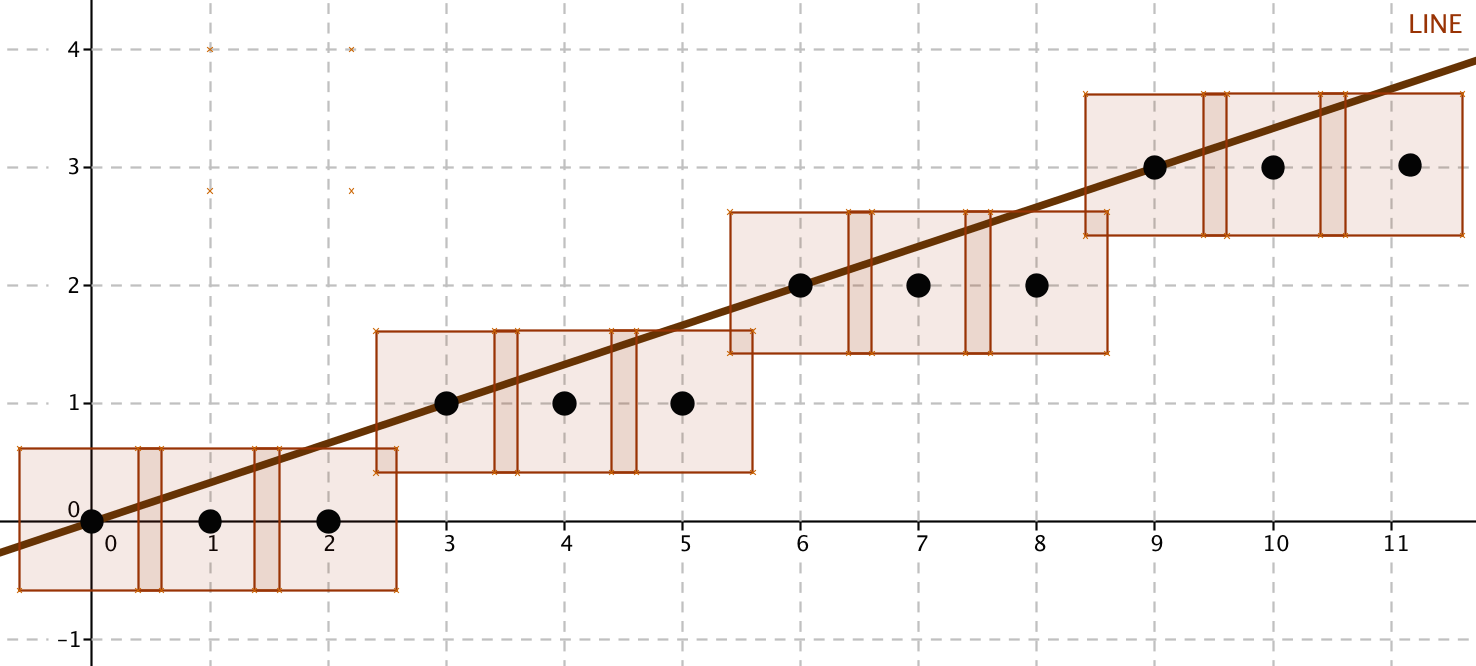
Abstract: Digital planes in all dimensions are studied, which means that digital straightness is in focus. The general goal is to generalize to any dimension the results of Kiselman's 2011 paper in Mathematika (Figure 23).
|
Convexity of Marginal Functions in the Discrete Case
Christer Kiselman
Partner: Shiva Samieinia, KTH
Funding: Stockholm University; KTH; Kingdom of Sweden
Period: 1011-
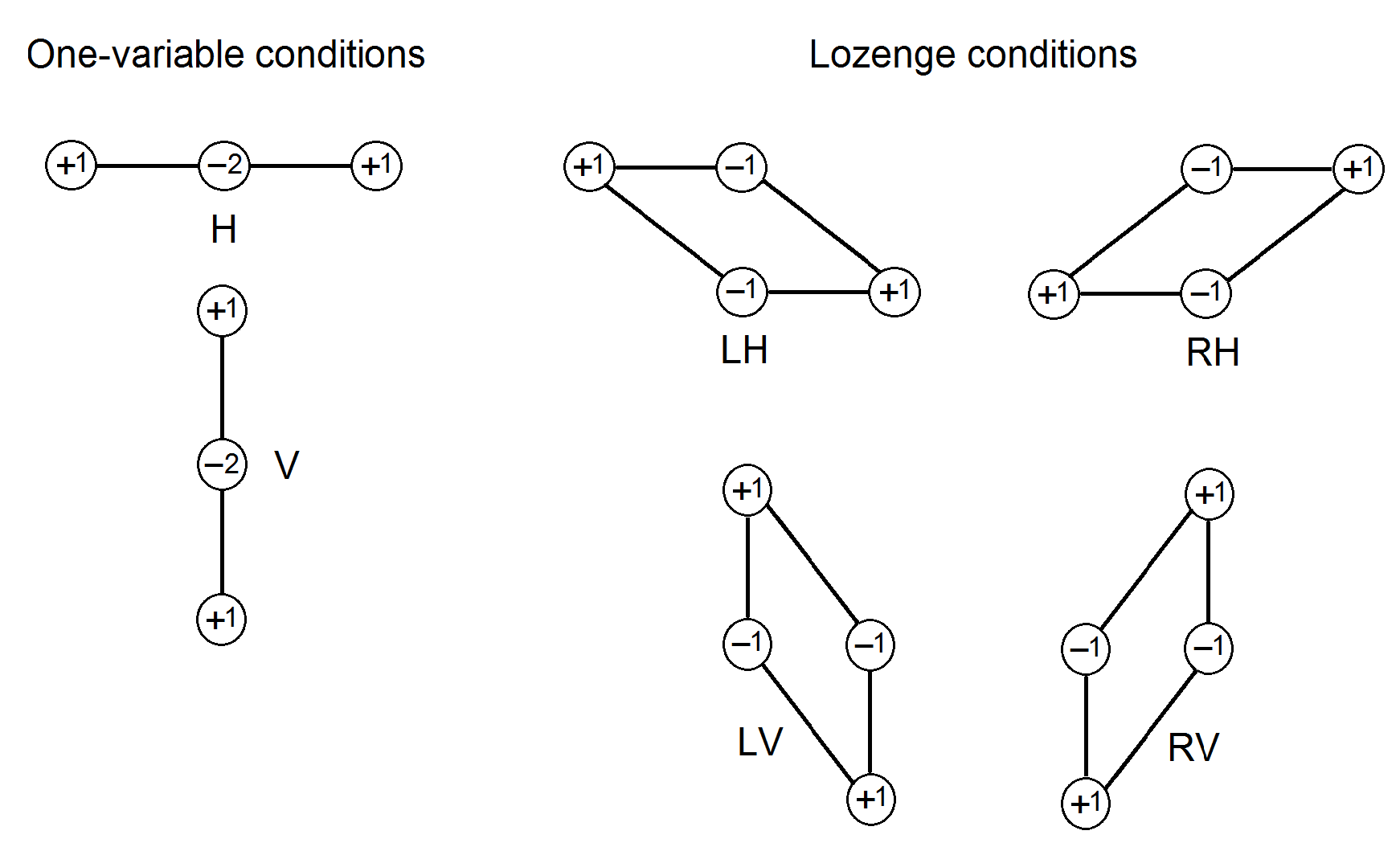
Abstract: We define, using difference operators, classes of functions defined on the set of points with integer coordinates which are preserved under the formation of marginal functions. The duality between classes of functions with certain convexity properties and families of second-order difference operators plays an important role and is explained using notions from mathematical morphology. A manuscript was submitted in 2014. Some problems remain to be solved (Figure 24).
|
Euclid's Straight Lines
Christer Kiselman
Funding: Kingdom of Sweden
Period: 0701-
Abstract: The project is both linguistic and mathematical. We raise two
questions on Euclid's Elements: How to explain that Propositions 16 and 27 in his first book do not follow, strictly speaking, from his postulates (or are perhaps meaningless)? and: What are the mathematical consequences of the meanings of the term eutheia, which we today often prefer to consider as different?
The answer to the first question is that orientability is a tacit assumption. The answer to the second is rather a discussion on efforts to avoid actual infinity, and having to (in some sense or another) construct equivalence classes of segments to achieve uniqueness. An article will appear in Normat.
Discrete Convolution Equations
Christer Kiselman
Funding: Kingdom of Sweden
Period: 1201-
Abstract: We study solvability of convolution equations for functions with discrete support in , a special case being
functions with support in the integer points. The more general case is of interest for several grids in Euclidean space, like the
body-centred and face-centered tesselations of three-space, as well
as for the non-periodic grids that appear in the study of
quasicrystals. The theorem of existence of fundamental solutions by de Boor, Höllig & Riemenschneider is generalized to general discrete supports, using only elementary methods. We also study the asymptotic
growth of sequences and arrays using the Fenchel transformation. Estimates using the Fourier transformation will be studied later.
DIPimage and DIPlib
Cris Luengo
Partners: Bernd Rieger, Lucas van Vliet, Quantitative Imaging Group, Delft University of Technology, The Netherlands; Michael van Ginkel, Unilever Research and Development, Colworth House, Bedford, UK
Funding: S-faculty, SLU
Period: 0807-1412
Abstract: DIPimage is a MATLAB toolbox for scientific image analysis, useful for both teaching and research (http://www.diplib.org). It has been in active development since 1999, when it was created at Delft University of Technology. In 2008, when Cris Luengo moved to Uppsala, CBA was added to the project as a main development site. DIPlib, created in 1995, is a C library containing many hundreds of image analysis routines. DIPlib is the core of the DIPimage toolbox, and both projects are developed in parallel. Because DIPlib provides efficient algorithms, MATLAB is useful for image analysis beyond the prototyping stage. Together, MATLAB and DIPimage form a powerful tool for working with scalar and vector images in any number of dimensions.
Versions 2.6 and 2.7 were released in 2014. Version 2.6 added the option to do arithmetic operations without changing the data type of the image, useful when working with very large images. We also fixed a major bug that appeared due to some undocumented internal change in MATLAB, which caused the output images of certain functions to be copied unnecessarily. Version 2.7 added the possibility to record macros (as MATLAB M-files), added a few new functions, and fixed many bugs. In particular, we had to make many changes for compatibility with MATLAB's new graphic system.
UPPMAX Cluster Computing
Petter Ranefall, Ida-Maria Sintorn, Carolina Wählby
Partners: Hans Karlsson, Elias Rudberg, Ola Spjuth, UPPMAX
Funding: SciLife Lab Uppsala; eSSENCE; Dept. of IT, UU
Period: 1110-
Abstract: Life science applications generate a huge amount of image data that has to be stored and analysed in an efficient way. This project
is focused on providing easy access to high-performance computers and large-scale storage. In collaboration with Uppsala Multidisciplinary Center for Advanced Computational Science (UPPMAX) image analysis software are being installed and maintained on the cluster. Database solutions with easy web access to image data are also being developed and maintained. This project has also provided workshops and seminars to help life science researchers to get started and use the resources. Several new large-scale image analysis projects using the computer cluster were initiated in 2014.